First of all, notice how the x-wing formation in this example includes two locked pairs: 7 & 3 on the top row, and 7 & 9 on the bottom row.
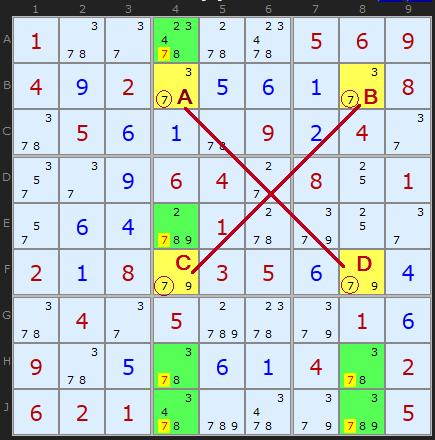
This means that on the top row, 7 must be either in B4 or B8. Those are the only possibilities. Let's start by observing what happens in each possible configuration for row B, the top of the x-wing formation.
Suppose B4, the top-left square in our x-wing configuration, is a 7. First, we'll cross out any numbers that are no longer valid in that row.
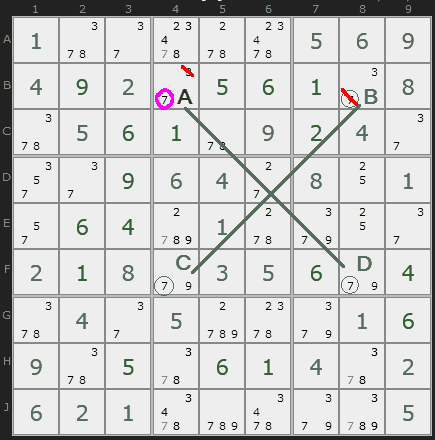
There is only one valid solution remaining for row B, so we'll fill those numbers in. Then we'll cross off the penciled-in 7s in column 4.
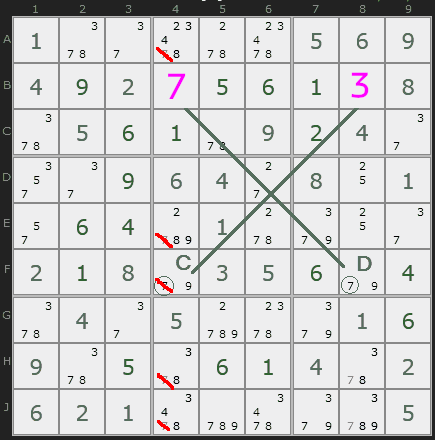
Only one possible number remains for square F4 -- the lower-left square in the x-wing rectangle. We'll fill that number in and cross out the other penciled-in 9 in the row.
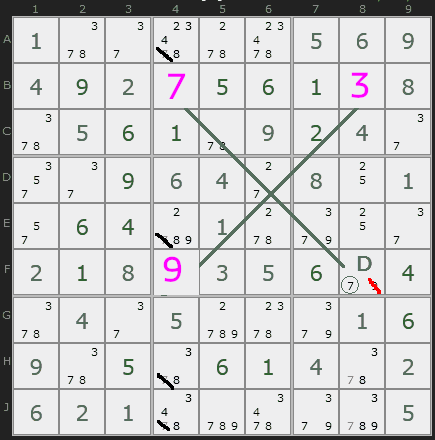
The only possible number for square F8 is 7. We will fill in that number and cross out any penciled-in 7s in the column, since there are none left in the row.
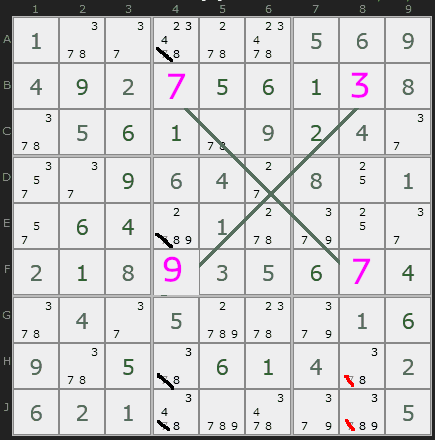
Now, let's say that B8, the upper-right square in our x-wing rectangle, is a 7.
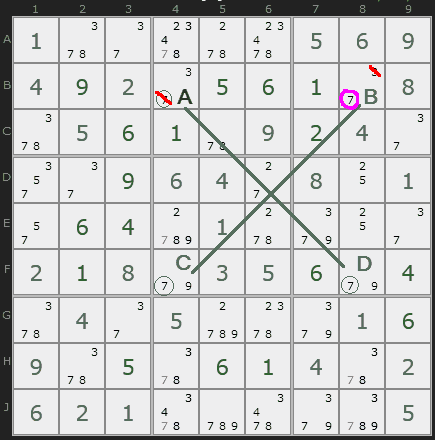
We'll fill in the solutions for row B since only one remains. The penciled-in 7s in column 8 can be eliminated.
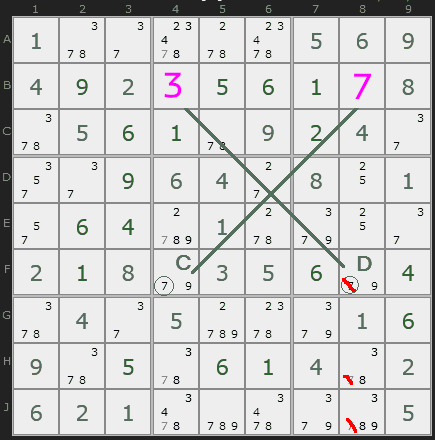
One valid answer remains for square F8, the lower-right x-wing square, so we'll fill that in and cross out the other penciled-in 9 in that row.
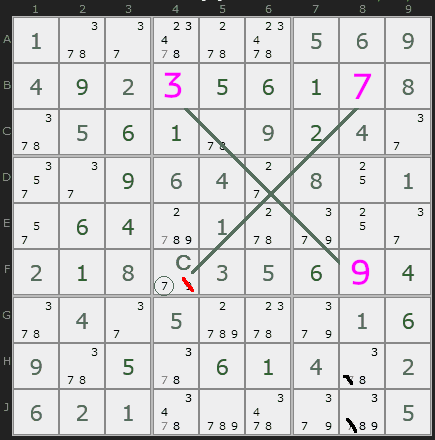
One answer remains for square F4, the last square in our x-wing configuration. We'll fill it in and cross out the invalid penciled-in numbers in that column.
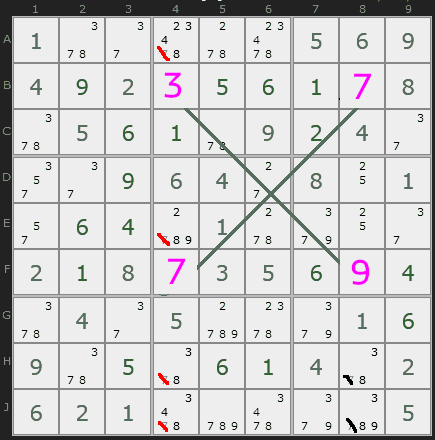
In either case, the penciled-in 7s in column 4 and column 8 can all be eliminated. You could test this out with the bottom row as well, but it shakes out the same as the illustrated cases. If square F8 were given to be 7, the outcome would be the same as that of case 1. If square F4 were given to be 7, the outcome would be the same as for case 2. There must be a 7 in two diagonal corners of the x-wing rectangle (either B4 and F8 or B8 and F4) because the top and bottom rows of the rectangle each have only two valid locations for a 7, and they can't be in the same column as each other.